ERIS - Travaux statistiques

"The essence of science is replication: a scientist should always be concerned about what would happen if he or another scientist were to repeat his experiment." (Guttman)

1. p_rep: Une nouvelle norme statistique

Depuis 2006, l'Association for Psychological Science a introduit dans les "author guidelines" de Psychological Science, une nouvelle norme de publication:

Statistics

Effect sizes should accompany major results. In addition, authors are encouraged to use prep rather than p values (see the article by Killeen in the May 2005 issue of Psychological Science, Vol. 16, pp. 345-353).

Killeen's p_rep (Killeen, 2005a) apparaît maintenant de manière routinière dans Psychological Science. Nous avons également trouvé son utilisation dans 15 autres revues [source: recherche dans Web of Science des articles citant Killeen (2005a), 24 avril 2008]:

Behavioral and Brain Functions
Cerebrovascular Diseases
Consciousness and Cognition
Developmental Psychology
European Journal of Cognitive Psychology
Evolution and Human Behavior
Human Communication Research
Journal of Experimental Psychology: Applied
Journal of Experimental Psychology: Learning, Memory, and Cognition
Journal of Memory and Language
Journal of Research in Personality
Language and Cognitive Processes
Perception
Psychonomic Bulletin & Review
The Quarterly Journal of Experimental Psychology

Il est essentiellement utilisé en association, soit avec un test t de Student de comparaison de moyennes soit avec un test F de l'analyse de variance avec un degré de liberté au numérateur. Nous nous limiterons donc à cette situation.

p_rep ("probability of replication") est la probabilité prédictive, conditionnellement aux données de l'expérience réalisée, de retrouver un effet de même signe dans une réplique de cette expérience. D'un point de vue pratique, elle peut être dérivée directement du seul seuil observé p; d'un point de vue formel, elle est donc équivalente à p. Mais elle a bien entendu une interprétation différente, puisqu'elle est une expression prédictive du résultat statistique de l'expérience.

p_rep peut être dérivée aussi bien par l'argument fiduciaire de Fisher que par un argument bayésien supposant une distribution initiale non informative (Killeen, 2005b).

Killeen, P.R. (2005a). An alternative to null-hypothesis significance tests. Psychological Science, 16, 345-353.
Killeen, P.R. (2005b). Replicability, Confidence, and Priors. Psychological Science, 16, 1009-1012.

Nous ne pouvons que nous réjouir du fait que pour la première fois une probabilité "naturelle" - c'est-à-dire une probabilité allant du connu (les données disponibles) vers l'inconnu (des observations à venir) - soit rapportée de manière routinière dans des revues de psychologie.
Cependant, sans parler d'autres usages possibles des probabilités fiducio-bayésiennes, cette pratique peut être améliorée, à la fois techniquement et conceptuellement.

Un examen attentif des articles publiés dans Psychological Science montre que de nombreux auteurs utilisent de façon incorrecte les formules disponibles. Ceci apparaît dû à une confusion entre les seuils observés p unilatéraux et bilatéraux, et révèle un sérieux problème de mise en oeuvre en pratique.

Nous avons trouvé que dans près de la moitié des articles publiés dans les deux numéros d'octobre 2006 et d'octobre 2007, p_rep était systématiquement sous-évaluée. En fait, pour la majorité d'entre eux, les valeurs données pouvaient être obtenues par l'une des formules données par Killeen si on les calculait (de manière erronée) en utilisant le seuil p bilatéral (au lieu du seuil unilatéral).

Les auteurs qui rapportent la probabilité prédictive p_rep se contentent de la juxtaposer à la statistique de test et/ou au seuil observé p. On peut craindre qu'eux et leurs lecteurs continuent de se focaliser sur la signification statistique des résultats. Cette attitude pourrait être renforcée par le fait, fortement suggéré par nos résultats experimentaux, que p_rep - la probabilité prédictive d'un résultat de même signe - pourrait être confondue avec la probabilité prédictive d'un résultat de même signe et significatif.

Seule une solution qui suppose une variance connue a été proposée et est actuellement utilisée. Plus de 100 ans après le célèbre article de Student (1906), on peut difficilement se satisfaire de cette restriction non nécessaire.

En traitant la variance comme inconnue, p_rep et p_srep, la probabilité d'une réplique significative au seuil unilatéral α, peuvent être calculées à partir de la distribution prédictive de la statistique de test t, ou, de manière équivalente, à partir de la distribution prédictive de l'effet standardisé ("Cohen's d"). Si nous désignons par t' la statistique de test dans la réplique, en supposant par exemple que t, la valeur observée dans l'expérience réalisée est positive, p_rep est la probabilité que t' soit positive et p_srep est la probabilité que t' soit supérieure à la valeur critique t_α, c'est-à-dire le 1-α percentile de la distribution de Student avec le même nombre de degrés de liberté que pour la statistique de test dans l'expérience réalisée.

La distribution fiducio-bayésienne prédictive de la statistique de test t été appelée une distribution K-prime dans Lecoutre (1984):

L'Analyse Bayésienne des Comparaisons

Elle est étudiée de manière détaillée dans Lecoutre (1999):

Two useful distributions for Bayesian predictive procedures under normal models

Un algorithme pour le calcul de sa fonction de répartition est donné dans Poitevineau et Lecoutre (2006):

Computing Bayesian predictive distributions: The K-square and K-prime distributions.

2. Calculer p_rep avec Excel

Dans le cas d'une variance connnue, Killeen (2005a) donne la formule suivante pour les utilisateurs d'Excel (version anglaise):

p_rep = NORMSDIST(NORMSINV(1-p)/SQRT(2)), où p est le seuil unilatéral du test z

d'où pour la version française d'Excel

p_rep = LOI.NORMALE.STANDARD((LOI.NORMALE.STANDARD.INVERSE(1-p))/RACINE(2))

Cette formule se généralise pour une variance inconnue, d'où respectivement pour les deux versions:

p_rep = 1-TDIST(TINV(2*p;dl)/SQRT(2);dl);1)

p_rep = 1-LOI.STUDENT((LOI.STUDENT.INVERSE(2*p;dl))/RACINE(2);dl;1)

où p est le seuil unilatéral du test t (pour un rapport F, diviser p par 2) et dl est le nombre de degrés de liberté

On peut aussi calculer directement à partir de la statistique de test, soit t de Student, d'où respectivement:

p_rep = 1-TDIST(ABS(t)/SQRT(2);dl;1)

p_rep = 1-LOI.STUDENT(ABS(t)/RACINE(2);dl;1)

soit rapport F avec un degré de liberté au numérateur, d'où respectivement:

p_rep = 1-TDIST(SQRT(F)/SQRT(2);dl;1)

p_rep = 1-LOI.STUDENT(RACINE(F)/RACINE(2);dl;1)

Ouvrir/Télécharger un fichier Excel pour le calcul de p_rep

3. Obtenir p_rep et p_srep à partir de tables

Table détaillée donnant p_rep en fonction du seuil bilatéral p

Afficher la table

Table détaillée donnant p_srep (pour α=.05) en fonction du seuil bilatéral p

Afficher la table

4. LePrep: un programme Windows convivial

la probabilité prédictive prep ("Killeen's probability of replication") de trouver un effet de même signe dans une réplique,

la probabilité prédictive psrep de trouver un effet de même signe et significatif au seuil unilatéral α dans une réplique,

la probabilité prédictive ppreprep de trouver un effet de même signe avec prep supérieur à γ dans une réplique.

Il peut aussi être utilisé comme une macro Word.

Estimation par intervalle pour un contrast: effet standardisé (calibré) ou brut

Distribution K-prime

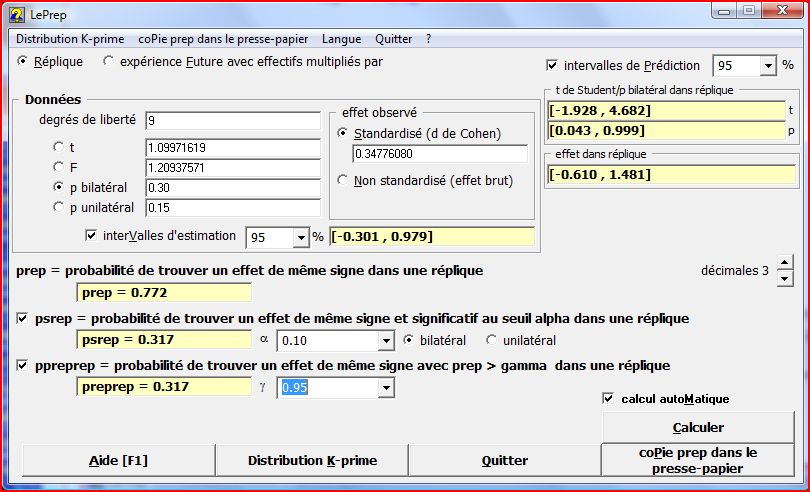
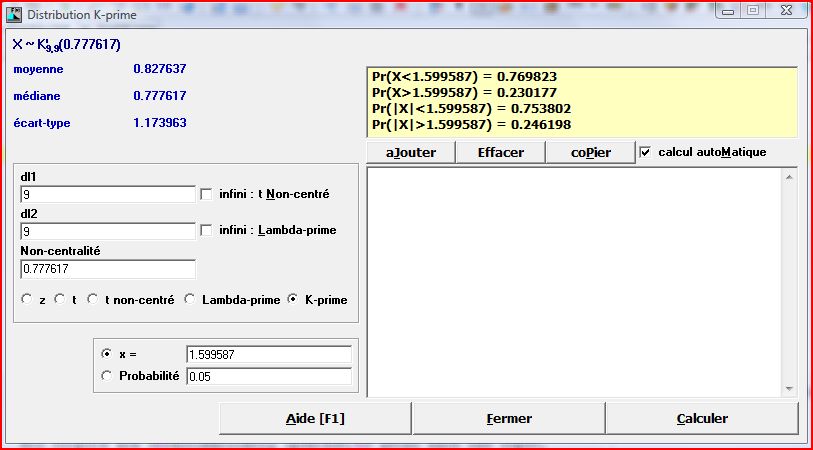
Télécharger LePrep [Windows]

5. Plus...

Voir:

Lecoutre, B., Lecoutre M.-P. & Poitevineau, J. (2010). Killeen’s probability of replication and predictive probabilities: How to compute, use and interpret them

Lecoutre & Killeen (2010). Replication is not coincidence: Reply to Iverson, Lee, and Wagenmakers (2009)

1. prep: Une nouvelle norme statistique

2. Calculer prep avec Excel

3. Obtenir prep et psrep à partir de tables

4. LePrep: un programme Windows convivial

5. Plus...

1. p_rep: Une nouvelle norme statistique

2. Calculer p_rep avec Excel

3. Obtenir p_rep et p_srep à partir de tables