Equipe Raisonnement Induction Statistique

"The essence of science is replication: a scientist should always be concerned about what would happen if he or another scientist were to repeat his experiment." (Guttman)
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |
In 2006, the Association for Psychological Science introduced in the
"author guidelines"
of Psychological Science a new norm of publication:
Statistics
Effect sizes should accompany major results. In addition, authors are
encouraged to use prep rather than p values (see the article by Killeen in the
May 2005 issue of Psychological Science, Vol. 16, pp. 345-353).
Killeen's prep (Killeen, 2005a) now routinely appears in Psychological Science. We also found its use in 15 other journals [Web of Science review of articles citing Killeen (2005a), april 24 2008]:
Behavioral and Brain Functions
Cerebrovascular Diseases
Consciousness and Cognition
Developmental Psychology
European Journal of Cognitive Psychology
Evolution and Human Behavior
Human Communication Research
Journal of Experimental Psychology: Applied
Journal of Experimental Psychology: Learning, Memory, and Cognition
Journal of Memory and Language
Journal of Research in Personality
Language and Cognitive Processes
Perception
Psychological science
Psychonomic Bulletin & Review
The Quarterly Journal of Experimental Psychology
![]() prep
("probability of replication") is the predictive probability,
given the data of the current experiment, to find again a same-sign effect in a replication of this experiment.
From a practical viewpoint, it can be derived from the observed p value only; consequently, from
a formal viewpoint, it is equivalent to p.
Of course it has a different interpretation, since it is a predictive expression
of the statistical result of the experiment.
prep
("probability of replication") is the predictive probability,
given the data of the current experiment, to find again a same-sign effect in a replication of this experiment.
From a practical viewpoint, it can be derived from the observed p value only; consequently, from
a formal viewpoint, it is equivalent to p.
Of course it has a different interpretation, since it is a predictive expression
of the statistical result of the experiment.
![]() prep
can be derived either from Fisher's fiducial argument as by a Bayesian
assuming noninformative priors (Killeen, 2005b).
prep
can be derived either from Fisher's fiducial argument as by a Bayesian
assuming noninformative priors (Killeen, 2005b).
Killeen, P.R. (2005a). An alternative to null-hypothesis significance tests.
Psychological Science, 16, 345-353.
Killeen, P.R. (2005b). Replicability, Confidence, and Priors.
Psychological Science, 16, 1009-1012.
We have enjoyed constating that for the first time a "natural" probability -
that is a probability going from the known (the data in hand)
to the unknown (observations to come) - was routinely reported in psychological journals.
However, without speaking of other uses of the fiducial-Bayesian probabilities, this practice
may be improved, both technically and conceptually.
![]() A careful examination of the articles published in Psychological Science revealed us that many authors
incorrectly used the available formulae, apparently confusing one-tailed and two-tailed p values.
This reveals a serious implementation problem.
A careful examination of the articles published in Psychological Science revealed us that many authors
incorrectly used the available formulae, apparently confusing one-tailed and two-tailed p values.
This reveals a serious implementation problem.
In about half articles published in the october issue for each of the two years 2006 and 2007, prep was found to be systematically undervalued. In the majority of these articles, the reported values could be obtained with the formulae given by Killen if we (erroneously) computed them with the two-tailed p value (instead of the one-tailed p value).
![]() The authors who report prep merely add it to the test statistic
and/or the p value. One can be afraid that they (and their readers) continue to focus
on the statistical significance of the results.
This attitude could be reinforced by the fact, strongly suggested by
our experimental findings,
that prep, the predictive probability of a same-sign result, could be confused
with the predictive probability of a same-sign and significant result.
The authors who report prep merely add it to the test statistic
and/or the p value. One can be afraid that they (and their readers) continue to focus
on the statistical significance of the results.
This attitude could be reinforced by the fact, strongly suggested by
our experimental findings,
that prep, the predictive probability of a same-sign result, could be confused
with the predictive probability of a same-sign and significant result.
Relaxing the assumption of known variance, prep and psrep, the probability
of a significant replication at one-tailed level
α,
can be computed from the predictive distribution of the test statistic
(or equivalently from the predictive distribution of Cohen's d).
If t2 denotes the test statistic in the replication, assuming for instance that
t1, the observed value in the current experiment is positive, prep is the probability
that t2 is positive and psrep is the probability that t2
exceeds
tα,
the 100α
percent upper point of the Student distribution with the same number of degrees of freedom as
for the test statistic in the current experiment.
![]() L'Analyse Bayésienne des Comparaisons
L'Analyse Bayésienne des Comparaisons
![]() Two useful distributions for Bayesian predictive procedures under normal models
Two useful distributions for Bayesian predictive procedures under normal models
![]() Computing Bayesian predictive distributions: The K-square and K-prime distributions.
Computing Bayesian predictive distributions: The K-square and K-prime distributions.
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |
prep = NORMSDIST(NORMSINV(1-p)/SQRT(2)), where p is the two tailed p value of the z test
prep = 1-TDIST(TINV(2*p,df)/SQRT(2),df),1)
where p is the two tailed p value of the t test (for an ANOVA F test, halve p) and df is the number of degrees of freedom.
prep can also be directly computed from the test statistic, either Student's t or ANOVA F with one degree of freedom in the numerator:prep = 1-TDIST(ABS(t)/SQRT(2),df,1)
prep = 1-TDIST(SQRT(F)/SQRT(2),df,1)
![]() Open/Download an Excel file for computing prep
Open/Download an Excel file for computing prep
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |
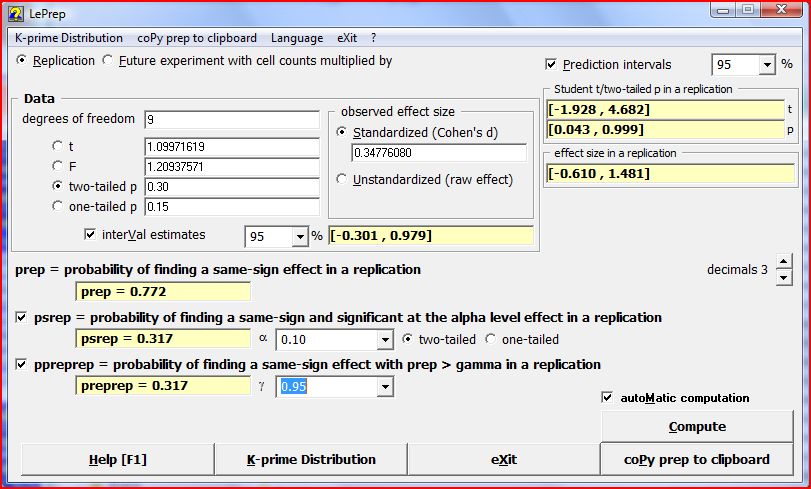
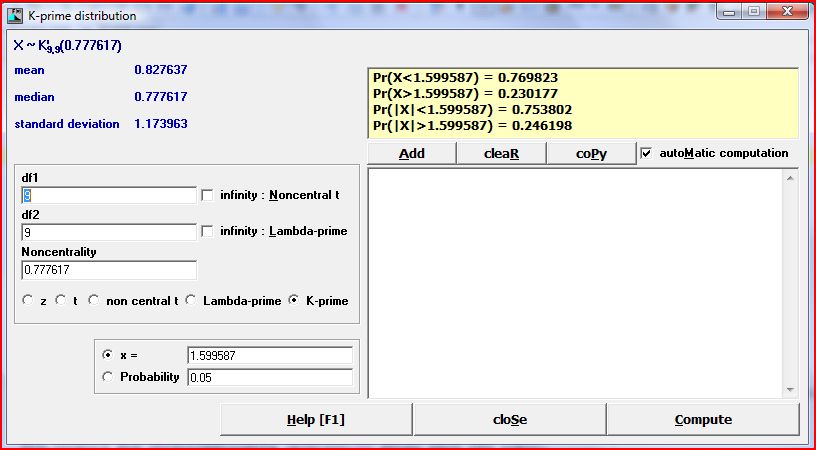
Download LePrep [Windows]
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |
Lecoutre, B., Lecoutre M.-P. & Poitevineau, J. (2010).
Killeen’s probability of replication and predictive probabilities: How to compute, use and interpret them
Lecoutre & Killeen (2010). Replication is not coincidence: Reply to Iverson, Lee, and Wagenmakers (2009)
|
prep A new statistical norm |
Computing prep with Excel |
Getting prep and psrep from tables |
LePrep A friendly-user Windows program |
More... |